1. 문제 상세
https://www.acmicpc.net/problem/24267
2. 문제 접근
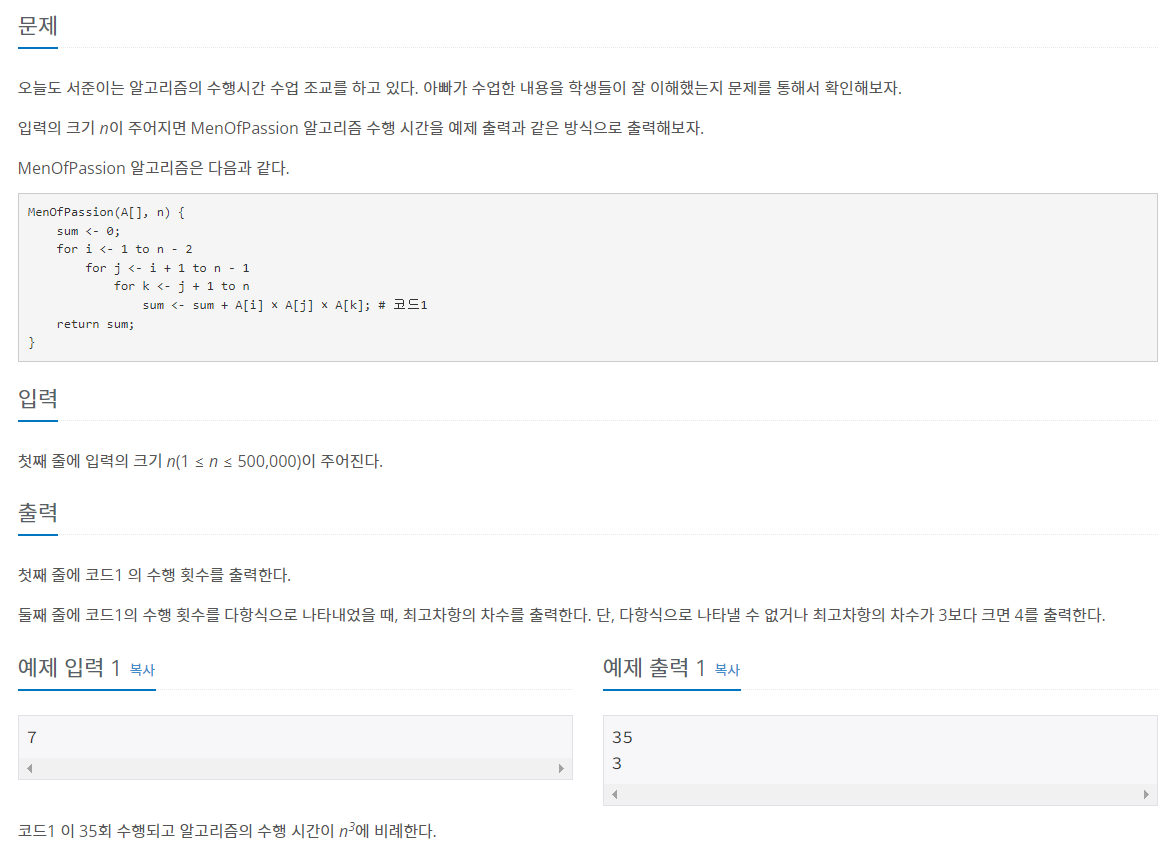
주어진 알고리즘을 보고 수행 횟수를 확인해보자.
이를 위해 예제를 통해 루프에서 i 와 j 의 상태를 확인해보자.
| i | j | k |
| 1 | 2 | 3, 4, 5, 6, 7 |
| 3 | 4, 5, 6, 7 | |
| 4 | 5, 6, 7 | |
| 5 | 6, 7 | |
| 6 | 7 | |
| 2 | 3 | 4, 5, 6, 7 |
| 4 | 5, 6, 7 | |
| 5 | 6, 7 | |
| 6 | 7 | |
| 3 | 4 | 5, 6, 7 |
| 5 | 6, 7 | |
| 6 | 7 | |
| 4 | 5 | 6, 7 |
| 6 | 7 | |
| 5 | 6 | 7 |
수행 횟수가 (5 + 4 +3 + 2 + 1) + (4 + 3 + 2 + 1) + (3 + 2 + 1) + (2 + 1) + 1 번 이라는 것을 알 수 있다.
이를 시그마 공식으로 변환하면
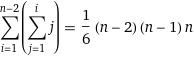
위와 같은 식으로 계산한다.
따라서 시간복잡도는 O(N3)이 되고, 수행 횟수는 항상 n(n - 1)(n - 2)/6 이 된다.
n 을 입력받고 n(n - 1)(n - 2)/6 과 차수인 3을 출력하자.
*주의사항, 이번에도 범위를 생각해서 int 형이 아닌 long 또는 long long 형으로 변수를 선언하여 사용하자.
3. 문제 풀이
#include <iostream>
using namespace std;
int main() {
long n;
cin >> n;
cout << n * (n - 1) * (n - 2) / 6 << endl << 3;
}
정수형(long 형) 변수 n 을 선언, cin 으로 정수를 입력받아 n 에 저장.
cout 으로 n * (n - 1) * (n - 2) / 6 값과 3을 출력.
4. 성능 확인

5. 마무리
'백준 - 단계별로 풀어보기 > 시간 복잡도' 카테고리의 다른 글
| [백준] 24313번 : 알고리즘 수업 - 점근적 표기 1 | C++ (0) | 2023.10.31 |
|---|---|
| [백준] 24266번 : 알고리즘 수업 - 알고리즘의 수행 시간 5 | C++ (0) | 2023.10.27 |
| [백준] 24265번 : 알고리즘 수업 - 알고리즘의 수행 시간 4 | C++ (0) | 2023.10.27 |
| [백준] 24264번 : 알고리즘 수업 - 알고리즘의 수행 시간 3 | C++ (0) | 2023.10.26 |
| [백준] 24263번 : 알고리즘 수업 - 알고리즘의 수행 시간 2 | C++ (0) | 2023.10.26 |
